
Maximizing the revenue of a battery energy storage system is achieved through an optimal battery dispatch strategy. The optimal dispatch involves maximizing revenue by exporting energy from the battery or available renewable production and minimizing energy purchased to charge the battery, subject to physical constraints of the battery and any import or export limitations. The optimization problem of interest can be expressed as follows:
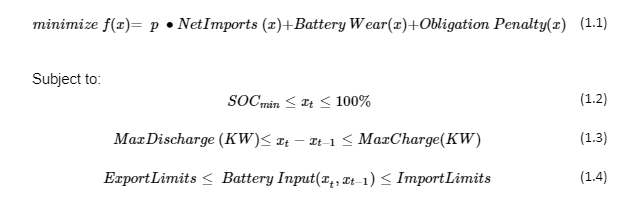
|
Term |
Description |
|
xt |
Battery state of charge (SOC) at timestep t |
|
P |
Energy market price |
|
Net imports |
The energy into or out of the system; net imports are negative when energy is exported, and positive when imported. This term reflects battery inputs, renewable production, converter and efficiency losses. |
|
Battery wear |
The wear cost depends on battery replacement cost and the battery charge or discharge at each timestep. |
|
Obligation Penalty |
Capacity market and time of delivery are treated as obligations that are penalized if not met. This term is 0 if capacity obligations are satisfied, positive otherwise. |
|
Import limits |
Available renewable production, interconnection limitations, as well as converter capacity limitations. |
|
Export limits |
Interconnection limitations and converter capacity limitations. |
|
|
|
Many theoretical algorithms are available for solving this class of inequality constrained optimization problems, where the proof of convergence requires meeting certain conditions at the solution. A nonlinear interior point method is used to solve this problem.
Dispatch Summary
Modeling battery dispatch involves the following steps:
i.Calculate the optimal dispatch over a 2-day horizon for a simplified battery model using the objective and constraints in Equation (1).
ii.Apply corrections to battery charge and discharge according to supplied battery model and apply degradation.
iii.Move optimization window forward 1 day using previous period to initialize the next window.
The dispatch is optimized over a two-day time horizon. The first 24 hours of the resulting dispatch are retained while the last 24 hours are used to initialize the next window. Using a time horizon that is longer than the optimization window ensures the battery has sufficient charge at the start of each period to take advantage of upcoming arbitrage opportunities and satisfy constraints.
The optimal dispatch incorporates several simplifications to the battery model to simplify the optimization problem. Then, a more exact model of the battery is applied to the optimized dispatch strategy to accurately model the system. For example, the charge and discharge constraints used in the optimization reflect the maximum possible charge and discharge the battery is capable of. Small adjustments are applied to the optimized dispatch to correct the charge and discharge according to the battery model parameters.
Additionally, battery degradation effects are not considered as dispatch decision variables. Degradation effects are applied to each time step of the supplied optimal dispatch instead. The 1-day optimization window is sufficiently small so that the applied degradation does not cause the modeled dispatch to significantly diverge from the optimized dispatch.
Multiple Energy Markets
Energy markets consist of one or more forward markets and an operational dispatching market. Forward energy markets include the day-ahead fifteen-minute markets. The real-time market, if present, is considered the operational market. In the absence of a real-time market, the last scheduled forward market is considered the operational market. The day-ahead market dispatch is scheduled first, followed by the fifteen-minute market and finally the real-time market. Operational adjustments are applied to the dispatch schedule as each market is optimized successively. The battery is dispatched according to the operational market schedule.
A portion of the overall system capacity may be withheld from forward market dispatches to guarantee additional capacity in later markets. This is achieved by restricting the battery state or charge bounds. For example, a two-market system with 50% of capacity reserved for the real-time market restricts the battery state of charge range to 25%-75% in the forward market dispatch. The battery is allowed to operate over its full range in the real-time market.
The market settlement is calculated according to the energy committed to each market. The day-ahead energy commitment is settled at the day-ahead market price and adjustments to the schedule in successive markets are settled at their market rates. The Front dispatch may buy-out of a scheduled position from a previous market. For example, it may be advantageous to buy-out of a selling position if the real-time price is lower than the day-ahead price. In this case, purchases in the real-time market include any purchases from the grid as well as buy-out of scheduled sales.
See Also